Ludibrium Irrealis
Ludibrium Irrealis

or “… alles andere ist Menschenwerk.”
We find ourselves in an apparently rules-bound universe. Things seem to happen consistently given the same initial conditions. As we’ve explored the world around us, we’ve found certain quantifiable parameters to have powerful, explanatory properties when applied in a given theoretical construct or model. Here we are considering two things. First, Newton’s laws of universal gravitation, which exist in space and time and concern the quantifiables of distance, mass, and velocity. Second, the limits of this theoretical structure.
As Norton’s Dome, introduced below, applies Newton’s laws in a situation contrived to thwart them, this work applies the dome in a situation that will explore, but inevitably fail to carry out its conclusions: it is made to exist in the real world. One must add that this attempt is far too coarse to be an actual experiment, but so would be any experiment. In fact, it is not possible to test.
✶
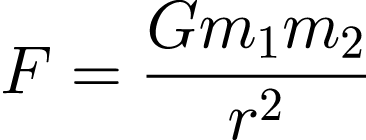
Science progresses through the making and testing of models. These models can be used to predict the results of experiments and verify our understanding of the world. But these models are also abstractions, simplifications. While thought experiments are processes to draw out either contradictions or inevitable consequences in scientific models; the former will sug- gest a need for revision, the latter may suggest actual experiments to confirm conclusions.
If all you care to do is predict the location of the planets in the night sky, Ptolemy’s model is as good as Kepler’s. Kepler’s simple ellipses will be easier to calculate than Ptolemy’s nested epicycles, but the results are the same. What is it to take the next step and propose a general law? It is the step from phenomenology to ontology—from describing appearances, to asserting something about the underlying nature of reality itself.
Newton’s proposition of universal gravitation and his mathematical model developed with the new method of calculus brought heaven and earth into one system—the simple falling of a stone and the orbits of the planets, all governed by the same law. The rules implied a mechanical universe that, once set in motion, would play out inevitably such that one could, in princi- ple, calculate from one instance all the past and future.
✶✶

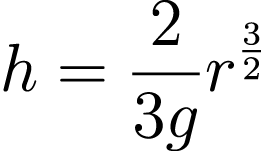
Norton’s Dome is a thought experiment exploring the limits of Newtonian mechanics developed by the philoso- pher of science John Norton. A unit point mass rests on the apex of a dome of a particular shape. The shape of the dome and the placement of the mass give a peculiar solution to Newton’s equations of motion. Either the mass stays there forever, or it begins to roll at any arbitrary time—not any random time, not on average once per hour, but any arbitrary time. Concluding that, at its limits, Newtonian mechanics cease to be deterministic, and movement requires no cause.
This scenario is physically impossible. Prosaically, it requires infinite precision in the fabrication of the dome and positioning of the mass. Abstracting a physical entity as a point mass doesn’t change the outcome of our calculations of planetary motion, but to work here, the dome’s surface must be infinitely ridged and without friction—neither can be the case in life. Additionally, we now know that Newton isn’t fundamental and will necessarily break down at its frontiers. There is no room for the indeterminacy of quantum mechanics which, for example, permits no perfect surfaces or even well-defined points!
So what can this tell us?
To the scientist, the result is not surprising—it is a scenario with an indeterminate solution that is incorrect in that it does not cohere with reality and whose incoherence is caused by its overgenerality. Rather than dwelling on the meaning, a scientist looks to what is missing, to the pathological simplifications that cause this result to diverge from reality. Mathematical models are only correct inasmuch as they are useful, and no model perfectly matches reality at all magnitudes, energies, or whatever parameters one may be concerned with.
To the philosopher of science, the inter- ests are different. How do we discern between what is scientific and what is not? When do generalizations become pathological and by what process does the divergence with reality happen? How close to reality can a model get?
✶✶✶
The first set of images considers the Dome itself as a reality—the model made actual, but necessarily imperfect, as are all material things. We watch as a ball rolls down the dome.
The second section is the experiment. The ball is released on the apex of the dome and may dwell or roll as it will, tracing out its path making the process measurable. Each exposure is a quarter of a second, which matches the time it takes the ball to roll down the dome.
Finally, the third section offers the result of this flawed experiment. This imperfect object was made and the motions of the experiment performed on something that cannot be in reality. Anything physical cannot reach the conclusion of an experiment that can only exist in pure abstraction. As such, rather than an arbitrary result, we conclude with a normal distribution.
And yet, for all this or despite it, it is only through abstraction that we can understand reality.
1. What might have been is an abstraction

2. Remaining a perpetual possibility

3. Only in a world of speculation
